Mohr's circle
Mohr's circle, named after Christian Otto Mohr, is a two-dimensional graphical representation of the state of stress at a point. The abscissa, 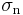 , and ordinate,
, and ordinate, 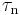 , of each point on the circle are the normal stress and shear stress components, respectively, acting on a particular cut plane with a unit vector
, of each point on the circle are the normal stress and shear stress components, respectively, acting on a particular cut plane with a unit vector 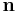 with components
with components 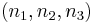 . In other words, the circumference of the circle is the locus of points that represent the state of stress on individual planes at all their orientations.
. In other words, the circumference of the circle is the locus of points that represent the state of stress on individual planes at all their orientations.
Karl Culmann was the first to conceive a graphical representation for stresses while considering longitudinal and vertical stresses in horizontal beams during bending. Mohr's contribution extended the use of this representation for both two- and three-dimensional stresses and developed a failure criterion based on the stress circle.[1]
Other graphical methods for the representation of the stress state at a point include the Lame's stress ellipsoid and Cauchy's stress quadric.
Contents |
Mohr's circle for two-dimensional stress states
A two-dimensional Mohr's circle can be constructed if we know the normal stresses 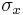 ,
, 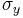 , and the shear stress
, and the shear stress 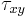 . The following sign conventions are usually used:
. The following sign conventions are usually used:
- Tensile stresses (positive) are to the right.
- Compressive stresses (negative) are to the left.
- Clockwise shear stresses are plotted upward.
- Counterclockwise shear stresses are plotted downward.
The reason for the above sign convention is that, in engineering mechanics[2], the normal stresses are positive if they are outward to the plane of action (tension), and shear stresses are positive if they rotate clockwise about the point in consideration. In geomechanics, i.e. soil mechanics and rock mechanics, however, normal stresses are considered positive when they are inward to the plane of action (compression), and shear stresses are positive if they rotate counterclockwise about the point in consideration.[1][3][4][5]
To construct the Mohr circle of stress for a state of plane stress, or plane strain, first we plot two points in the  space corresponding to the known stress components on both perpendicular planes, i.e.
space corresponding to the known stress components on both perpendicular planes, i.e. 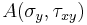 and
and 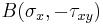 (Figure 1 and 2). We then connect points
(Figure 1 and 2). We then connect points 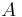 and
and 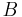 by a straight line and find the midpoint
by a straight line and find the midpoint 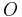 which corresponds to the intersection of this line with the
which corresponds to the intersection of this line with the 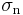 axis. Finally, we draw a circle with diameter
axis. Finally, we draw a circle with diameter 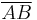 and centre at
and centre at 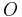 .
.
The radius 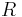 of the circle is
of the circle is ![R = \sqrt{\left[\tfrac{1}{2}(\sigma_x - \sigma_y)\right]^2 %2B \tau_{xy}^2}\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/1fcdd1b2cf3db0c152af80f8c32fe2b1.png) , and the coordinates of its centre are
, and the coordinates of its centre are ![\left[\tfrac{1}{2}(\sigma_x %2B \sigma_y), 0\right]\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/373f9b807e104e77cd4039ba1b97e609.png) .
.
The principal stresses are then the abscissa of the points of intersection of the circle with the 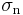 axis (note that the shear stresses are zero for the principal stresses).
axis (note that the shear stresses are zero for the principal stresses).
Drawing a Mohr's circle
The following procedure is used to draw a Mohr's circle and to find the magnitude and direction of maximum stresses from it.
- First, the
 - and
- and  -axes of a Cartesian coordinate system are identified as the
-axes of a Cartesian coordinate system are identified as the 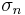 -axis and
-axis and 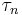 -axis, respectively.
-axis, respectively. - Next, two points of the Mohr's circle are plotted. These are the points B (
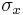 ,
, 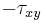 ) and A (
) and A (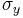 ,
, 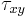 ). The line connecting these two points is a diameter of the Mohr's circle.
). The line connecting these two points is a diameter of the Mohr's circle. - The center of the Mohr's circle, O, is located where the diameter, AB, intersects the σ-axis. This point gives the average normal stress (σavg). The average normal stress can be read directly from a plot of the Mohr's circle. Alternatively, it can be calculated using
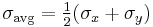 .
.
- The Mohr's circle intersects the
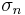 axis at two points, C and E. The stresses at these two end points of the horizontal diameter are
axis at two points, C and E. The stresses at these two end points of the horizontal diameter are 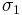 and
and 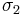 , the principal stresses. The point
, the principal stresses. The point 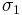 represents the maximum normal stress (σmax) and the point
represents the maximum normal stress (σmax) and the point 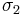 is the minimum normal stress (σmin). The equations for finding these values are
is the minimum normal stress (σmin). The equations for finding these values are
- Next we examine the points where the circle intersects the line parallel to
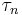 -axis passing through the center of the circle, O. The vertical diameter of the circle passes through O (σavg) and goes up to positive
-axis passing through the center of the circle, O. The vertical diameter of the circle passes through O (σavg) and goes up to positive 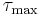 and down to negative
and down to negative 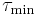 . The magnitudes of extreme values are equal to the radius of the Mohr's circle, but with different signs. The equation to find these extreme values of the shear stress is[6]
. The magnitudes of extreme values are equal to the radius of the Mohr's circle, but with different signs. The equation to find these extreme values of the shear stress is[6]
![\tau_{\max,\min}= \pm \sqrt{\left[\tfrac{1}{2}(\sigma_x- \sigma_y)\right]^2%2B {\tau_{xy}}^2}](/2012-wikipedia_en_all_nopic_01_2012/I/5e19c30e7376a357246f6e515cb53f43.png) .
.
- The next value to determine is the angle that the plane of maximum normal stress makes with the
 -axis. Let us create a new
-axis. Let us create a new  -axis by drawing a line from the center of the Mohr circle, O, through point A. Let the angle between the
-axis by drawing a line from the center of the Mohr circle, O, through point A. Let the angle between the  -axis and the
-axis and the  -axis be
-axis be  . If
. If  is the angle between the maximum normal stress and the
is the angle between the maximum normal stress and the  -axis, then it can be shown that
-axis, then it can be shown that  = 2
= 2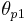 . The angle
. The angle  is found by:
is found by:
![\phi = 2\theta_{p1} = \arctan\left[2\tau_{xy}/(\sigma_x- \sigma_y)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/424f8cb0061c918a90b5bf7ff418b924.png) .
.
- To find the angle that the direction that the plane of maximum shear stress makes with the
 -axis, we use the relation
-axis, we use the relation
![2\theta_s = \arctan\left[-(\sigma_x - \sigma_y)/(2\tau_{xy})\right]](/2012-wikipedia_en_all_nopic_01_2012/I/1541660135d6390a03d01747918a4098.png) . It is important to pay attention to the use of these two equations as they look similar.
. It is important to pay attention to the use of these two equations as they look similar.
- Often, the final step of the process is to also draw a square stress element indicating the orientations of the maximum normal and shear stresses; the normal stress element at an angle
 and the maximum shear stress element at an angle of
and the maximum shear stress element at an angle of 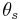 .
.
The previous discussion assumes, implicitly, that there are two orthogonal directions  and
and  that define a plane in which the stress components
that define a plane in which the stress components 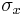 .
. 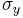 , and
, and 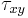 are known. It is also implicit that these stresses are known at a point
are known. It is also implicit that these stresses are known at a point 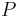 in a continuum body under plane stress or plane strain. The Mohr circle, once drawn, can be used to find the components of the stress tensor for any other choice of orthogonal directions in the plane.
in a continuum body under plane stress or plane strain. The Mohr circle, once drawn, can be used to find the components of the stress tensor for any other choice of orthogonal directions in the plane.
Stress components on an arbitrary plane
Using the Mohr circle one can find the stress components 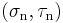 on any other plane with a different orientation
on any other plane with a different orientation 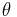 that passes through point
that passes through point 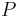 . For this, two approaches can be used:
. For this, two approaches can be used:
- The first approach relies on the fact that the angle
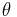 between two planes passing through
between two planes passing through 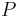 is half the angle between the lines joining their corresponding stress points
is half the angle between the lines joining their corresponding stress points 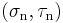 on the Mohr circle and the centre of the circle (Figure 1). In other words, the stresses
on the Mohr circle and the centre of the circle (Figure 1). In other words, the stresses 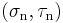 acting on a plane at an angle
acting on a plane at an angle 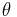 counterclockwise to the plane on which
counterclockwise to the plane on which 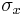 acts is determined by traveling counterclockwise around the circle from the known stress point
acts is determined by traveling counterclockwise around the circle from the known stress point 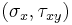 a distance subtending an angle
a distance subtending an angle 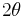 at the centre of the circle (Figure 1).
at the centre of the circle (Figure 1). - The second approach involves the determination of a point on the Mohr circle called the pole or the origin of planes. Any straight line drawn from the pole will intersect the Mohr circle at a point that represents the state of stress on a plane inclined at the same orientation (parallel) in space as that line. Therefore, knowing the stress components
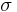 and
and 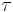 on any particular plane, one can draw a line parallel to that plane through the particular coordinates
on any particular plane, one can draw a line parallel to that plane through the particular coordinates 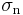 and
and 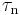 on the Mohr circle and find the pole as the intersection of such line with the Mohr circle. As an example, let's assume we have a state of stress with stress components
on the Mohr circle and find the pole as the intersection of such line with the Mohr circle. As an example, let's assume we have a state of stress with stress components 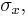 ,
, 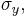 , and
, and 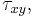 , as shown on Figure 2. First, we can draw a line from point
, as shown on Figure 2. First, we can draw a line from point 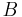 parallel to the plane of action of
parallel to the plane of action of 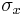 , or, if we choose otherwise, a line from point
, or, if we choose otherwise, a line from point 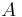 parallel to the plane of action of
parallel to the plane of action of 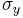 . The intersection of any of these two lines with the Mohr circle is the pole. Once the pole has been determined, to find the state of stress on a plane making an angle
. The intersection of any of these two lines with the Mohr circle is the pole. Once the pole has been determined, to find the state of stress on a plane making an angle 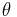 with the vertical, or in other words a plane having its normal vector forming an angle
with the vertical, or in other words a plane having its normal vector forming an angle 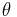 with the horizontal plane, then we can draw a line from the pole parallel to that plane (See Figure 2). The normal and shear stresses on that plane are then the coordinates of the point of intersection between the line and the Mohr circle.
with the horizontal plane, then we can draw a line from the pole parallel to that plane (See Figure 2). The normal and shear stresses on that plane are then the coordinates of the point of intersection between the line and the Mohr circle.
Mohr's circle for a general three-dimensional state of stresses
To construct the Mohr's circle for a general three-dimensional case of stresses at a point, the values of the principal stresses 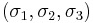 and their principal directions
and their principal directions 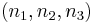 must be first evaluated.
must be first evaluated.
Considering the principal axes as the coordinate system, instead of the general 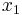 ,
, 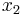 ,
, 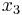 coordinate system, and assuming that
coordinate system, and assuming that 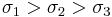 , then the normal and shear components of the stress vector
, then the normal and shear components of the stress vector 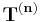 , for a given plane with unit vector
, for a given plane with unit vector 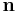 , satisfy the following equations
, satisfy the following equations
Knowing that 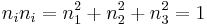 , we can solve for
, we can solve for 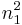 ,
, 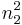 ,
, 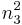 , using the Gauss elimination method which yields
, using the Gauss elimination method which yields
Since 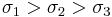 , and
, and 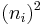 is non-negative, the numerators from the these equations satisfy
is non-negative, the numerators from the these equations satisfy
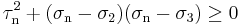 as the denominator
as the denominator 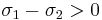 and
and 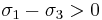
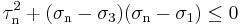 as the denominator
as the denominator 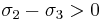 and
and 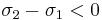
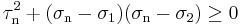 as the denominator
as the denominator 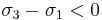 and
and 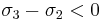
These expressions can be rewritten as
which are the equations of the three Mohr's circles for stress 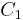 ,
, 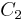 , and
, and 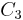 , with radii
, with radii 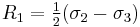 ,
, 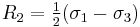 , and
, and 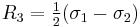 , and their centres with coordinates
, and their centres with coordinates ![\left[\tfrac{1}{2}(\sigma_2 %2B \sigma_3), 0\right]\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/86cb9f6e824b978918a2e484b673d7ea.png) ,
, ![\left[\tfrac{1}{2}(\sigma_1 %2B \sigma_3), 0\right]\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/c5b8f547ccae7405b3d520dd15577a7e.png) ,
, ![\left[\tfrac{1}{2}(\sigma_1 %2B \sigma_2), 0\right]\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/35d467ab2ffec0d91fbbbc6a72293990.png) , respectively.
, respectively.
These equations for the Mohr's circles show that all admissible stress points 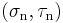 lie on these circles or within the shaded area enclosed by them (see Figure 3). Stress points
lie on these circles or within the shaded area enclosed by them (see Figure 3). Stress points 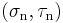 satisfying the equation for circle
satisfying the equation for circle 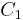 lie on, or outside circle
lie on, or outside circle 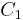 . Stress points
. Stress points 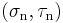 satisfying the equation for circle
satisfying the equation for circle 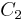 lie on, or inside circle
lie on, or inside circle 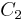 . And finally, stress points
. And finally, stress points 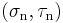 satisfying the equation for circle
satisfying the equation for circle 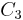 lie on, or outside circle
lie on, or outside circle 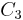 .
.
References
- ^ a b Parry
- ^ The sign convention differ in disciplines such as mechanical engineering, structural engineering, and geomechanics. The engineering mechanics sign convention is used in this article.
- ^ Jumikis
- ^ Holtz
- ^ Brady
- ^ Megson, T.H.G., Aircraft Structures for Engineering Students, Fourth Edition, 2007, section 1.8
Bibliography
- Beer, Ferdinand Pierre; Elwood Russell Johnston, John T. DeWolf (1992). Mechanics of Materials. McGraw-Hill Professional. ISBN 0-07-112939-1.
- Brady, B.H.G.; E.T. Brown (1993). Rock Mechanics For Underground Mining (Third ed.). Kluwer Academic Publisher. pp. 17–29. ISBN 0-412-47550-2. http://books.google.ca/books?id=s0BaKxL11KsC&lpg=PP1&pg=PA18#v=onepage&q=&f=false.
- Davis, R. O.; Selvadurai. A. P. S. (1996). Elasticity and geomechanics. Cambridge University Press. pp. 16–26. ISBN 0-521-49827-9. http://books.google.ca/books?id=4Z11rZaUn1UC&lpg=PP1&pg=PA16#v=onepage&q=&f=false.
- Holtz, Robert D.; Kovacs, William D. (1981). An introduction to geotechnical engineering. Prentice-Hall civil engineering and engineering mechanics series. Prentice-Hall. ISBN 0-13-484394-0. http://books.google.ca/books?id=yYkYAQAAIAAJ&dq=inauthor:%22William+D.+Kovacs%22&ei=kF-MS5LRKpfCM9vEhIYN&cd=1.
- Jaeger, John Conrad; Cook, N.G.W, & Zimmerman, R.W. (2007). Fundamentals of rock mechanics (Fourth ed.). Wiley-Blackwell. pp. 9–41. ISBN 0-632-05759-9. http://books.google.com/books?id=FqADDkunVNAC&lpg=PP1&pg=PA10#v=onepage&q=&f=false.
- Jumikis, Alfreds R. (1969). Theoretical soil mechanics: with practical applications to soil mechanics and foundation engineering. Van Nostrand Reinhold Co.. ISBN 0-442-04199-3. http://books.google.ca/books?id=NPZRAAAAMAAJ&source=gbs_navlinks_s.
- Parry, Richard Hawley Grey (2004). Mohr circles, stress paths and geotechnics (2 ed.). Taylor & Francis. pp. 1–30. ISBN 0-415-27297-1. http://books.google.ca/books?id=u_rec9uQnLcC&lpg=PP1&dq=mohr%20circles%2C%20sterss%20paths%20and%20geotechnics&pg=PA1#v=onepage&q=&f=false.
- Timoshenko, Stephen P.; James Norman Goodier (1970). Theory of Elasticity (Third ed.). McGraw-Hill International Editions. ISBN 0-07-085805-5.
- Timoshenko, Stephen P. (1983). History of strength of materials: with a brief account of the history of theory of elasticity and theory of structures. Dover Books on Physics. Dover Publications. ISBN 0-486-61187-6.
![\sigma_1 = \sigma_\max = \tfrac{1}{2}(\sigma_x %2B \sigma_y) %2B \sqrt{\left[\tfrac{1}{2}(\sigma_x- \sigma_y)\right]^2%2B \tau_{xy}^2}](/2012-wikipedia_en_all_nopic_01_2012/I/33e900e386829720ecce7cb89c04a7f8.png)
![\sigma_2 = \sigma_\min = \tfrac{1}{2}(\sigma_x %2B \sigma_y) - \sqrt{\left[\tfrac{1}{2}(\sigma_x- \sigma_y)\right]^2%2B \tau_{xy}^2}](/2012-wikipedia_en_all_nopic_01_2012/I/b3c9288784215dab9733e5c72b2cccd3.png)
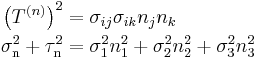
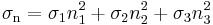
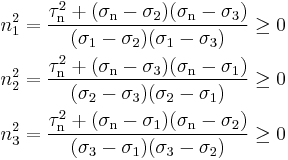
![\begin{align}
\tau_\mathrm{n}^2 %2B \left[ \sigma_\mathrm{n}- \tfrac{1}{2} (\sigma_2 %2B \sigma_3) \right]^2 \ge \left( \tfrac{1}{2}(\sigma_2 - \sigma_3) \right)^2 \\
\tau_\mathrm{n}^2 %2B \left[ \sigma_\mathrm{n}- \tfrac{1}{2} (\sigma_1 %2B \sigma_3) \right]^2 \le \left( \tfrac{1}{2}(\sigma_1 - \sigma_3) \right)^2 \\
\tau_\mathrm{n}^2 %2B \left[ \sigma_\mathrm{n}- \tfrac{1}{2} (\sigma_1 %2B \sigma_2) \right]^2 \ge \left( \tfrac{1}{2}(\sigma_1 - \sigma_2) \right)^2 \\
\end{align}\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/33821591d920ac61b7b475ef18e44909.png)